Применение геометрических средних для отчетов о прошлых результатах.

Для отчетности на основе исторических ставок доходности геометрическое среднее более привлекательно, чем среднее арифметическое, потому что оно представляет собой темп роста или ставку доходности, которую мы должны были бы получать каждый год, чтобы соответствовать фактическим, совокупным инвестиционным показателям.

Например, в упрощенном Примере (2) средней геометрической и арифметической доходности мы приобрели акцию за €100, при этом 2 года спустя она стоила также  €100, а 1 год спустя -  €200.

Среднее геометрическое значение доходности здесь - 0%. Очевидно, что оно представляет собой сложный темп роста (сложную процентную ставку) за двухлетний период. В частности, конечная сумма является начальной суммой, умноженной на \( (1 + R_G)^2 \). Среднее геометрическое является отличным показателем прошлых результатов.

Пример, упомянутый выше, иллюстрирует, как среднее арифметическое может исказить нашу оценку исторических показателей. В этом примере совокупная доходность за двухлетний период однозначно равна 0%. Но, при 100% доходности за первый год и -50% за второй, среднее арифметическое составляет 25%.

Как мы уже отмечали ранее, среднее арифметическое всегда больше или равно среднему геометрическому.

Если мы хотим оценить среднюю доходность за 1 период, мы должны использовать среднее арифметическое, потому что среднее арифметическое - это среднее значение доходности за 1 период. Однако, если мы хотим оценить среднюю доходность за более чем 1 период, нам следует использовать среднюю геометрическую доходность, поскольку среднее геометрическое отражает то, как ставки доходности за период образуют совокупную доходность за несколько периодов.

Как следствие использования геометрического среднего для отчетов о доходности, полулогарифмические (англ. 'semilogarithmic scale'), а не арифметические шкалы измерений более подходят для построения графиков прошлых результатов. В контексте отчетности об инвестиционных результатах полулогарифмический график имеет арифметическую шкалу на горизонтальной оси для времени и логарифмическую шкалу на вертикальной оси для стоимости инвестиций.

Значения на вертикальной оси отмечены в соответствии с различиями между их логарифмами.

Предположим, мы хотим представить £1, £10, £100 и £1,000 в качестве стоимости инвестиций на вертикальной оси.

Обратите внимание, что каждое последующее значение представляет 10-кратное увеличение по сравнению с предыдущим значением, и каждое из них будет равномерно отмечено на вертикальной оси, поскольку разница в их логарифмах составляет примерно 2.30. То есть:

 \(\ln10 - \ln1 = \ln100 - \ln10 = \ln1,000 - \ln100 = 2.30 \)

В полулогарифмическом масштабе равные деления на вертикальной оси отражают одинаковые процентные изменения, а рост инвестиций с постоянной процентной ставкой представляет на графике прямую линию.

Кривая, изгибающаяся вверх, отражает увеличение темпов роста с течением времени.

Изгибы кривой в разных точках можно сравнивать, чтобы судить об относительных темпах роста.

Применение арифметических средних для финансовых прогнозов.

В дополнение к отчетам о прошлых результатах финансовым аналитикам необходимо прогнозировать ожидаемые премии за риск по акциям. Для этой цели лучше подходит среднее арифметическое.

Мы можем проиллюстрировать использование среднего арифметического в перспективном контексте на примере, основанном на будущих денежных потоках инвестиций. При дисконтировании будущих денежных потоков, существенная проблема связана с неопределенностью.

Предположим, что инвестор, распоряжающийся $100,000 сталкивается с равной вероятностью (50/50) 100-процентной или -50-процентной доходности, как показано на древовидной диаграмме. При 100-процентной доходности в одном периоде и -50-процентном доходе в другом, среднее геометрическое доходности составляет:

\( \sqrt {2(0.5)} - 1 = 0 \)

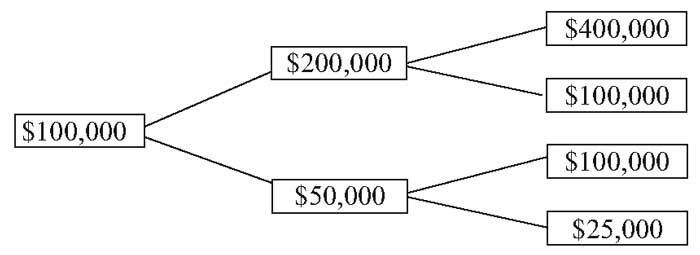Древовидная диаграмма инвестиционных решений. Древовидная диаграмма инвестиционных решений.

Средняя геометрическая доходность 0% дает моду или медиану дохода после двух периодов (т.е. конечный доход или доход на конец рассматриваемого периода) и, таким образом, точно предсказывает модальный или медианный конечный доход в этом примере.

Тем не менее, среднее арифметическое лучше предсказывает конечный доход. При равных шансах доходности 100% или -50% рассмотрим 4 одинаково вероятных результата в $400,000, $100,000, $100,000 и $25,000, как если бы они действительно имели место.

Средний арифметический конечный доход составил бы:

$156,250 = ($400,000 + $100,000 + $100,000 + $25,000) / 4.

Фактическая доходность составила бы 300%, 0%, 0% и -75% при средней арифметической доходности за 2 периода:

(300 + 0 + 0 -75) / 4 = 56.25%.

Это средняя арифметическая доходность предсказывает конечный доход в размере $100,000 \( \times \) 1.5625 = $156,250. Отметив, что 56.25% для двух периодов составляют 25% за период, мы должны затем дисконтировать ожидаемый конечный доход в размере $156,250 по средней арифметической ставке 25%, чтобы отразить неопределенность в денежных потоках.

  • Неопределенность в денежных потоках или доходности приводит к тому, что среднее арифметическое будет больше среднего геометрического.
  • Чем более неопределенны доходы, тем больше расхождение между средними арифметическими и геометрическими значениями.
  • Средняя геометрическая доходность приблизительно равна средней арифметической доходности за вычетом половина дисперсии доходности.

Нулевая дисперсия или нулевая неопределенность в доходах оставляют геометрическую и арифметическую доходность примерно равными, но в условиях реальной неопределенности среднеарифметическая доходность больше, чем среднегеометрическая.

Например, для номинальной годовой доходности S&P 500 с 1926 по 2012 год в Таблице 27 приведено среднее арифметическое значение 11.82% и стандартное отклонение 20.18%.

Среднее геометрическое значение этих ставок доходности составляет 9.84%. Мы можем видеть, что среднее геометрическое приблизительно равно среднему арифметическому за вычетом половины дисперсии доходности:

\( R_G \approx 0.1182 - (1/2) (0.2018^2) = 0.0978 \) или 9.78%.