В предыдущей теме мы обсуждали, как определить, отличается ли распределение доходности от нормального распределения из-за асимметрии.

Еще одна причина, из-за которой распределение может отличаться от нормального распределения, заключается в том, что большее количество доходов может быть сконцентрировано близко к среднему значению (более пиковое распределение) и большее количество доходов может сильнее отклоняется от среднего (у распределения более толстые хвосты).

По сравнению с нормальным распределением, такое распределение имеет большую долю незначительных отклонений от среднего дохода (больше мелких неожиданностей) и большую долю экстремально больших отклонений от среднего дохода (больше больших неожиданностей). Большинство инвесторов воспринимают большую вероятность очень больших отклонений от среднего как повышенный риск.

Эксцесс или крутизна распределения (англ. 'kurtosis') - это статистическая мера, которая сигнализирует нам, что распределение более или менее пиковое, по сравнению с нормальным распределением.

  • Распределение с более острой вершиной, чем обычно, называется островершинным или лептокуртическим (англ. 'leptokurtic', от греческого слова lepto - узкий).
  • Распределение, более сглаженное, чем обычно, называется плосковершинным или платикуртическим  (англ. 'platykurtic', от греческого слова platy - широкий);
  • Распределение, идентичное нормальному распределению отношении крутизны вершины, называют распределением с нормальным эксцессом или мезокуртическим (англ. 'mesokurtic', от греческого слова meso - средний).

Описанная нами ситуация с более частыми экстремально большими наблюдениями  - это островершинное наблюдение.

График, представленный ниже, иллюстрирует островершинное распределение. Оно имеет более острую вершину и более толстые хвосты, чем нормальное распределение.

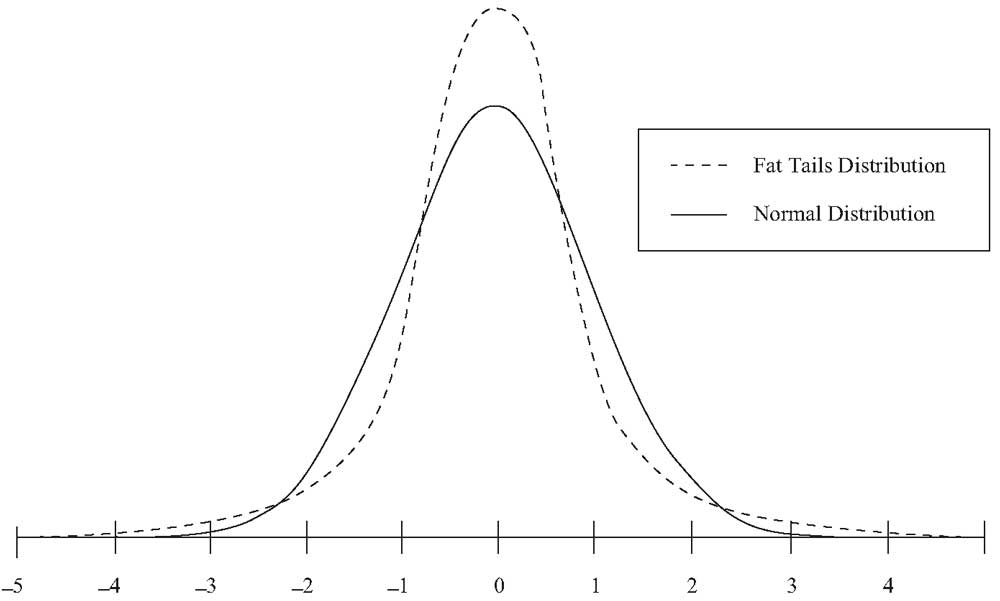Рисунок 8. Островершинное распределение с толстыми хвостами. Рисунок 8. Островершинное распределение с толстыми хвостами.

Расчет коэффициента эксцесса включает в себя определение среднего отклонения от среднего, возведенного в четвертую степень, а затем деление результата на стандартное отклонение, возведенное в четвертую степень.

Эта мера не привязана к шкале. Значение эксцесса всегда положительно, потому что отклонения возведены в четвертую степень.

Для всех нормальных распределений эксцесс равен 3. Многие статистические программные пакеты рассчитывают избыточный эксцесс, как эксцесс минус 3.

Избыточный эксцесс (англ. 'excess kurtosis'), таким образом, характеризует эксцесс относительно нормального распределения:

  • Распределение с нормальным эксцессом имеет эксцесс равный 0. 
  • Островершинное распределение имеет избыточный эксцесс больше 0.
  • Плосковершинное распределение имеет избыточный эксцесс меньше 0.

Распределение доходности с положительным избыточным эксцессом (островершинное распределение доходности) - имеет больше экстремально больших отклонений от среднего значения, чем нормальное распределение.

Формула избыточного эксцесса выборки.

Ниже приведена формула для расчета выборочного избыточного эксцесса (англ. 'sample excess kurtosis'):

(Формула 18)

\( \dst
K_E = \left( {n(n+1) \over (n-1)(n-2)(n-3)} {\dsum_{i=1}^n (X_i - \overline X)^4 \over s^4} \right) - {3(n-1)^2 \over (n-2)(n-3)} \)

где

  • \( n \) - размер выборки, а
  • \(s\) - стандартное отклонение выборки.

В Формуле 18 выборочный эксцесс - первый член. Обратите внимание, что когда n становится большим, Формула 18 приблизительна равна:

\( \begin{aligned} {n^2 \over n^3} {\sum (X - \overline X)^4 \over s^4} - {3n^2 \over n^2} = {1 \over n} {\sum (X - \overline X)^4 \over s^4} - 3 \end{aligned} \)

Для выборки из 100 наблюдений или больше, при нормальном распределении, избыточный эксцесс выборки равный 1.0 или больше будет считаться необычно большим.

Было обнаружено, что большинство рядов доходности акций являются островершинными. Если обратное распределение имеет положительный избыточный эксцесс (лептокуртоз) и мы используем статистические модели, которые не учитывают более толстые хвосты, мы будем недооценивать вероятность очень плохих или очень хороших результатов.

Например, доходность S&P 500 за 19 октября 1987 года составляла 20 стандартных отклонений от средней дневной доходности. Такой результат возможен при нормальном распределении, но его вероятность почти равна 0.

Если ежедневные ставки доходности взяты из нормального распределения, то

  • доходность в 4 стандартных отклонения или более ожидается раз в 50 лет;
  • доходность в 5 стандартных отклонений или более ожидается каждые 7000 лет.

Доходность за октябрь 1987 года, скорее всего, была получена из распределения с более толстыми хвостами, чем у нормального распределения.

Если посмотреть на Таблицу 27, приведенную ранее, то в месячной доходности индекса S&P 500 наблюдается очень большой избыточный эксцесс, приблизительно 9.4. Это чрезвычайно толстый хвост по сравнению с нормальным распределением. В отличие от месячной доходности, ряд годовой доходности почти не имеет избыточного эксцесса.

Результаты по избыточному эксцессу согласуются с результатами исследований, согласно которым нормальное распределение является лучшим приближением для доходности акций США с годовым периодом владения, чем для доходности с более короткими (например, месячным) периодами владения.

Следующий пример иллюстрирует расчет избыточного эксцесса выборки для одного из двух взаимных фондов, рассмотренных ранее.

Пример расчета выборочного избыточного эксцесса доходности.

Сделав вывод о том, что годовая доходность фонда T. Rowe Price Equity Income была отрицательно ассиметрична в течение периода 2003-2012 гг., что мы можем сказать об эксцессе распределения доходности фонда?

В Таблице 28 (повторно) приводятся годовые доходы фонда.

Таблица 28. Годовая доходность T. Rowe Price Equity Income, 2003-2012 гг. (повторно)

Год

Доходность (%)

2003

25.78

2004

15.05

2005

4.26

2006

19.14

2007

3.30

2008

-35.75

2009

25.62

2010

15.15

2011

-0.72

2012

17.25

Используя информацию из Таблицы 28, сделайте следующее:

  1. Рассчитайте избыточный эксцесс PRFDX с точностью до двух десятичных знаков.
  2. Охарактеризуйте форму распределения доходности PRFDX на основе вашего ответа на часть 1 как лептокуртическую, мезокуртическую или платикуртическую.

Решение для части 1:

Чтобы вычислить избыточный эксцесс, мы находим сумму отклонений от среднего значения, возведенных в четвертую степень, делим ее на стандартное отклонение, возведенное в четвертую степень, и затем умножаем полученный результат на \( n (n + 1) / [(n - 1 ) (n - 2) (n - 3)]\). Этот расчет определяет эксцесс.

Избыточный эксцесс - это эксцесс минус \( 3 (n - 1)^2 / [(n - 2) (n - 3)] \).

В Tаблице 30 приведены соответствующие расчеты.

Таблица 30. Расчет эксцесса для PRFDX.

Год

\(R_t\)

\( R_t - \overline R \)

\( (R_t - \overline R)^4 \)

2003

25.78

16.87

80,995.395

2004

15.05

6.14

1,421.260

2005

4.26

-4.65

467.533

2006

19.14

10.23

10,952.229

2007

3.30

-5.61

990.493

2008

-35.75

-44.66

3,978,092.479

2009

25.62

16.71

77,966.098

2010

15.15

6.24

1,516.137

2011

-0.72

-9.63

8,600.133

2012

17.25

8.34

4,837.981

n =

10

R =

8.91%

Сумма =

4,165,839.738

s =

18.12%

s4 =

107,803.478

Сумма/s4 =

38.643

n(n + 1)/[(n - 1)(n - 2)(n -3)] =

0.2183

Эксцесс =

8.434

3(n - 1)2/[(n - 2)(n -3)] =

4.34

Избыточный эксцесс =

4.09

Источник: performance.morningstar.com.

Используя Формулу 18, делаем расчет:

\( \dst K_E = {110 \over (9)(8)(7)} {4,165,839.738 \over 18.12^4} - {3(9)^2 \over (8)(7)} = 4.09 \)

Решение для части 2:

Распределение годовой доходности PRFDX, по-видимому, является островершинным, исходя из положительного избыточного эксцесса выборки. Довольно большой избыточный эксцесс 4.09 указывает на то, что распределение годовой доходности PRFDX имеет толстые хвосты относительно нормального распределения.

С отрицательной асимметрией и положительным избыточным эксцессом, похоже, что годовая доходность PRFDX не распределялась нормально в течение периода.